이번 포스트에서는 "Top-𝐾 Off-Policy Correction for a REINFORCE Recommender System" (https://arxiv.org/pdf/1812.02353.pdf)라는 논문을 소개하고자 한다.
Introduction
Objective
- 아이템 추천으로 유저의 장기적인 만족도를 최대화할 수 있는 RL Agent 학습
Challenges
- Large, non-stationary state and action space: 추천시스템 문제를 MDP로 모델링하기 위해 유저의 취향을 state, 추천할 아이템을 action으로 정의한다. 유저의 취향은 매우 복잡하고 시간에 따라 변한다. 아이템의 개수는 무수히 많고 새로운 아이템이 계속 유입된다.
- Off-policy training : 다른 RL 문제와 달리 self-play나 시뮬레이션을 통해 학습 데이터를 생산할 수 없다. 이전 추천시스템들로 생성된 실제 유저에 대한 실제 추천 데이터로 학습해야한다.
- Top-K recommendation : Top-1이 아닌 Top-K recommendation에 적합한 알고리즘 필요하다.
MDP Modeling
추천시스템을 강화학습 세팅에 적합하게 모델링해보자. 각 유저에 대하여, 추천시스템이 그동안 취한 action(추천한 아이템)과 그에 대한 해당 유저의 피드백(클릭, 시청 시간, etc.)의 sequence가 주어졌다고 하자. 이를 이용하여 유저의 만족도 지표(클릭 수, 시청 시간 등)를 높일 수 있는 추천시스템의 다음 action(다음에 추천할 아이템)을 예측해야한다. 이 문제는 MDP(Markov Decision Process)로 나타낼 수 있다.

결국 강화학습의 목표는 reward-to-go를 최대화할 수 있는 policy \(\pi (aㅣs)\)를 찾는 것이다. 구체적으로 \(\pi (aㅣs)\)는 유저의 state \(s \in S\)가 주어졌을 때 action/item \(a\)를 추천할 확률을 의미한다.
\(\theta\)로 parameterize된 policy를 \(\pi_{\theta}\)라고 했을 때 policy gradient는 다음과 같이 계산된다.

여기서 \(d_t^{\pi}\)는 policy가 \(\pi\)일 때 시간 t의 discounted state visitation frequency이고, \(R_t(s_t, a_t)\)는 시간 t의 discounted future reward이다.

Model Architecture

유저의 과거 시퀀스 \(\tau = (s_0, a_0, s_1, ...)\)를 RNN으로 처리하여 유저의 다음 state vector의 예측값 \(s_{t+1}\)을 구한다. 그리고 각 action/item \(a \in A\)의 임베딩 \(v_a\)를 구한다. 마지막으로 아래와 같은 softmax를 통해 \(t+1\)에서의 policy \(\pi_{\theta}(a_{t+1}, s_{t+1})\)를 출력한다.

Off-Policy Correction
앞서 언급했듯이 추천시스템에서는 시뮬레이터가 아닌 실제 유저 데이터를 사용해야하기 때문에 현재 policy로 생성한 학습 데이터를 얻기 힘들다. 대신 과거 policy나 다른 추천시스템과 상호작용한 유저 데이터로 학습해야 한다. 그러므로 on-policy 학습이 불가능하다. 학습 데이터를 생성하는데 실제로 사용된 추천시스템의 policy를 behavior policy라고 부르고 \(\beta\)라고 표기하자. 그러면 importance sampling에 의해 policy gradient는 다음과 같이 바뀐다.

하지만 이 policy gradient로 학습시키면 \(\pi_{\theta}\)와 \(\beta\)의 차이가 클 때 variance가 매우 커질 수 있다. Variance를 줄이기 위해 위의 식을 다음과 같이 근사하였다고 한다.
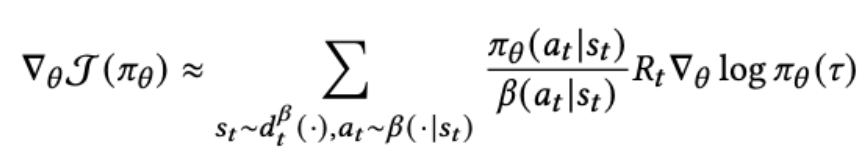
여기서 문제가 발생한다. 위 gradient를 계산하려면 \(\beta\)의 파라미터를 알아야 한다. 이는 추정할 수 밖에 없다.
학습 데이터에 있는 모든 state-action pair \((s,a)\)를 이용하여 유저 상태가 \(s\)일 때 action이 \(a\)일 확률을 예측하도록 \(\beta_{\theta'}\)을 학습시킨다. 리워드로 학습하는 것이 아니라 supervised 방식으로 학습시키는 것이다. \(s\)를 임베딩할 유저 state vector의 경우 RNN의 output을 재사용하고 추천 action에 대한 확률은 새로운 softmax layer를 통해 출력하도록 한다. 그리고 \(\beta_{\theta'}\)가 RNN parameter update에 영향을 주지 않게 하기 위해 그림에서처럼 gradient를 block한다.
학습 데이터를 생성하는데 하나가 아닌 여러 policy가 사용되었을 수도 있다. 지금 학습시키고 있는 추천시스템의 과거 policy들일 수도 있고, 다른 추천시스템과 상호작용한 유저의 기록들일 수도 있다. 이 경우 \(\beta_{\theta'}\)를 여러 추천시스템을 앙상블한 policy라고 해석할 수 있다.
Top-K Recommendation
우리의 추천시스템은 하나의 아이템이 아니라 유저가 관심을 가질만한 K개의 아이템을 추천해서 유저가 그 중에서 고를 수 있도록 해야한다. Softmax policy \(\pi_{\theta}\)로 각 아이템을 독립적으로 샘플링하고 중복된 아이템은 제거하는 방식으로 K개의 아이템을 선택한다고 하자. 그러면 어떠한 아이템 a가 선택된 K개의 아이템 중 하나일 확률은 다음과 같다.

그러면 policy gradient는 아래와 같다.

Policy gradient에 off-policy correction을 하면 아래 식과 같아진다.

하나의 아이템을 추천할 때의 off-policy correction된 policy gradient를 다시 한번 살펴보자.

결국 Top-K recommendation에서의 off-policy correction이 된 policy gradient는 top-1에서의 off-policy correction된 policy gradient에 다음이 곱해진 것이다.

이 \(\lambda_K(s,a)\)를 자세히 살펴보자.

두번째 특징에 의해 한 아이템에 추천 확률이 몰릴 경우 그 아이템에 대한 policy gradient가 0에 가까워져 더 이상 추천 확률이 증가하지 않도록 한다. 이에 따라 추천 확률이 특정 아이템에 집중되지 않고 여러 아이템에 분산된다.
Exploration
- Epsilon-Greedy : 추천의 질을 떨어뜨리기 때문에 본 문제에는 적합하지 않다.
- Sampling K Items from \(\pi_{\theta}\) (가장 확률이 높은 K개의 아이템을 선택하는 대신): 전체 softmax를 계산해야 하는데 아이템 수/action space가 크기 때문에 computation cost가 크다.
대안
가장 큰 확률의 \(M (M >> K)\)개의 아이템을 선택한 후 그들의 logit을 이용하여 softmax normalization을 한다. 이렇게 얻은 분포에서 \(K\)개의 아이템을 샘플링한다. 실제로는 exploration과 exploitation을 balance하기 위하여 가장 확률이 높은 \(K'\)개의 아이템을 먼저 선택한 후 나머지 \(K-K'\)개의 아이템을 \(M-K'\)개의 아이템 중에서 샘플링했다고 한다.
Experiment Results
Simulation
Off-Policy Correction의 중요성
10개의 아이템 1,...,10이 있고 아이템 1을 추천했을 때의 리워드는 1, 2를 추천했을 때의 리워드는 2, ..., 10을 추천했을 때의 리워드는 10이다. Optimal policy는 아이템 10을 계속 추천하는 것이다.

위 차트는 학습 데이터를 생성하는 behavior policy를 \(\beta(a_i) = \frac{11-i}{55}\)(\(i\)는 아이템 번호)로 했을 때 모델이 학습한 policy를 나타낸다. 수식에서 알 수 있듯이 \(\beta\)는 리워드가 낮은 아이템일 수록 추천할 확률이 높도록 하는 policy이다. 왼쪽 그래프는 off-policy correction이 없었을 때 모델이 학습한 policy, 오른쪽 그래프는 off-policy correction을 했을 때 모델이 학습한 policy이다. 오른쪽의 경우 거의 1의 확률로 아이템 10을 추천하는, 거의 optimal한 policy이지만 왼쪽의 경우 suboptimal하다.
Top-K Correction의 중요성
10개의 아이템이 있고, 아이템 1을 추천했을 때의 리워드는 10, 아이템 2를 추천했을 때의 리워드는 9, 그리고 나머지 아이템을 추천했을 때의 리워드는 1이다. 이번에는 두 개의 아이템을 추천하는 것이 목적이다 (K = 2). 학습할 때 behavior policy \(\beta\)는 uniform distribution을 선택했다고 한다.

왼쪽 차트는 그냥 off-policy correction을 했을 때 학습된 policy를 나타내고 오른쪽 차트는 Top-2 off-policy correction을 했을 때 학습된 policy를 나타낸다. 그냥 off-policy correction을 한 경우 reward가 가장 높은 아이템 1을 추천할 확률만 거의 1이고 나머지는 거의 0이다. 가장 좋은 한 개의 아이템 밖에 학습 못한 것이다. 반면 Top-2 off-policy correction을 한 경우 아이템 1,2를 추천할 확률 모두 어느 정도 높다.
Live
- 유튜브 RNN candidate generator에 의해 추려진 아이템들에 REINFORCE 알고리즘 적용
- 4~10시간에 거친 long-term reward
- 새로운 이벤트가 발생할 때마다 continuous training(24시간 미만의 지연)
Off-Policy Correction의 중요성
- Control : Off-policy correction을 안 한 모델을 적용한 traffic
- Experiment : \(\pi_{\theta}\)와 \(\beta_{\theta'}\)을 모두 학습하여 off-policy correction을 한 모델을 적용한 traffic
Experiment 내에서 인기가 낮은 영상들이 선택되는 비율이 Control보다 거의 3배 더 높았다. Off-policy correction을 안 하면 학습된 policy가 behavior policy 하에 많이 선택되었던 컨텐츠 위주로 추천하기 때문에 결국 인기가 높은 컨텐츠만 더 추천되는 "rich get richer" 현상이 일어난다고 저자들은 설명한다. Control과 Experiment 사이에 시청 시간 차이는 별로 없었지만, 시청한 영상의 개수의 경우 Experiment가 0.53% 더 많았다고 한다.
Top-K Correction의 중요성
Top-16 off-policy correction을 한 모델을 적용한 traffic에서 그냥 off-policy correction을 한 모델을 적용한 traffic에 비해 시청 시간이 약 0.85% 더 길었다고 한다.
'추천시스템' 카테고리의 다른 글
| 랭킹 최적화 문제 (0) | 2022.07.18 |
|---|---|
| 정형 데이터를 다루기 위한 Neural Network (0) | 2022.01.18 |
| Sequential Recommendation과 GNN (0) | 2022.01.18 |
| 추천시스템과 GNN(Graph Neural Network) (0) | 2022.01.18 |
| DQN 기반 추천시스템 (0) | 2022.01.18 |



