TabNet: Attentive Interpretable Tabular Learning (https://arxiv.org/pdf/1908.07442.pdf) 내용 정리
문제 제기
딥러닝은 이미지, 자연어 등 비정형 데이터를 처리하는데는 좋은 성과를 보였지만 정형 데이터(tabular data) 관련 분야에서는 그러지 못하였다. CNN, FC layer 등은 표를 다루는데 적합하지 않다. 정형 데이터 관련해서는 아직까지는 ensemble decision tree 계열의 알고리즘들이 가장 많이 사용된다. 그렇다면 왜 굳이 딥러닝을 정형 데이터 처리에 적용하려고 하는 것일까? 저자들은 정형 데이터 처리에 있어서 딥러닝(gradient descent 기반의 end-to-end learning)의 이점을 다음과 같이 주장한다.
- 이미지 등 다른 비정형 데이터를 정형 데이터와 함께 처리하기 좋다.
- Decision tree 기반 알고리즘들에 비해 feature engineering에 들어가는 노력을 많이 줄일 수 있다.
- 실시간 데이터로부터 학습하는데 용이하다.
- Domain adaptation, generative modeling, semi-supervised learning 등에 적용할 수 있는 representation을 학습할 수 있다.
저자들은 TabNet이라는 정형 데이터 처리를 위한 딥러닝 모델을 개발하였다. TabNet은 전처리 과정 없이 raw tabular data를 바로 입력으로 받으며 gradient descent 기반의 최적화 알고리즘으로 학습된다.
알고리즘 설명

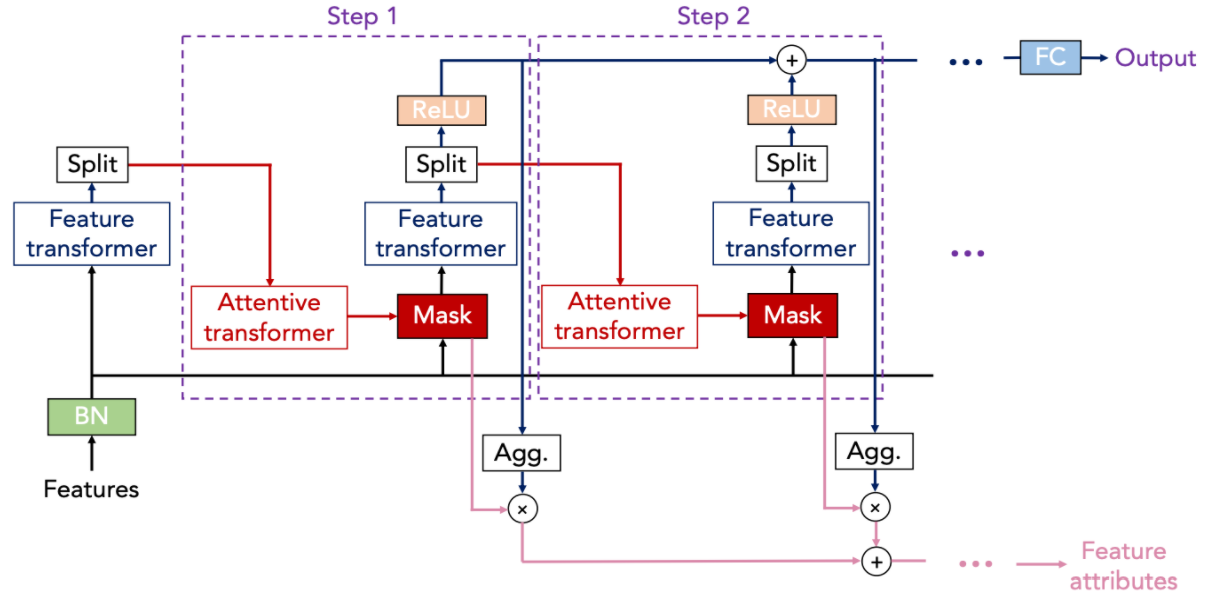
TabNet의 큰 그림을 이해하기 위해서 위 그림의 예시를 살펴보자.
TabNet은 \(N_{steps}\)개의 decision step을 순차적으로 거쳐 output을 도출한다. 한 decision step은 sparse instance-wise feature selection 과정과 input processing 과정으로 이루어졌다. 각 decision step마다 고려할 feature를 선택한 후 neural net으로 처리하는 것이다.
그림에서 주어진 데이터의 전체 attribute의 집합은 {age, workclass, education, marital.status, occupation, relationship, race, sex, capital.gain, capital.loss, hours.per.week, native.country}이다. 그림에는 두 개의 decision step이 묘사되어 있다. 첫 번째 step에서 TabNet은 직업과 관련된 feature인 workclass, education, occupation, hours.per.week만 선택하여 처리하기로 했다. 해당 step에서의 output은 최종 결과값에 합산될 output과 다음 decision step으로 보낼 output으로 나뉜다. 두 번째 step에서 TabNet은 이전 step에서 보낸 정보를 토대로 이번에는 이 사람의 투자와 관련된 feature인 capital.gain과 capital.loss만 선택하여 처리하기로 했다. 처리 결과를 담은 정보는 또 다음 step으로 전달되고, 그 step에서는 또 다른 feature들을 선택하면서 총 Nsteps번의 feedback loop가 돌아간다. 마지막 decision step이 끝난 다음 TabNet은 모든 decision step의 output을 aggregate하여 최종 결과값을 도출한다. 그림에서 결과값은 이 사람의 소득이 5만불을 넘는가에 대한 binary 예측값이다.
전체적인 과정을 보면 TabNet이 decision tree의 특징을 많이 갖고 있음을 느낄 것이다. 첫 번째로 TabNet은 sparse instance-wise feature selection, 즉 각 data point 별로 필요한 feature만 선택하여 처리한다. 어떠한 feature를 선택할지는 데이터로부터 학습한다. 두 번째로 TabNet은 sequential multi-step 구조를 갖고 있으며 모든 step의 output을 고려하여 최종 결정을 내리는 방식으로 앙상블과 같은 효과를 낸다. 마지막으로 선택한 feature의 non-linear 처리를 통해 풍부한 함수 표현이 가능하다.
이제 네트워크를 더 구체적으로 살펴보자.
Input Features
표의 숫자형 데이터와 학습 가능한 파라미터들로 임베딩된 categorical feature들의 concatenation에 batch normalization을 수행한 결과값이 매 decision step의 input이 된다. 이 vector의 notation을 앞으로 f라고 하자.
Feature Selection
\(i\)번째 decision step에서는 attentive transformer가 \((i-1)\)번째 decision step의 정보를 받아 어떠한 feature를 select할지 결정한다. 구체적으로 각 step마다 input에 적용할 mask M[i]를 도출한다.

a[i-1]은 이전 decision step에서 온 정보이다. $h_i$는 (FC Layer + Batch Normalization)이다. P[i-1]은 해당 feature가 이전 decision step들에서 얼마나 사용되었는지 나타내는 scaling term이다. 구체적인 식은 아래와 같다.

\(\gamma\)가 1이면 각 feature를 오직 한 번의 decision step에서만 사용하도록 하겠다는 것을 의미한다. \(\gamma\)가 1보다 크면 좀더 유연하게 한 feature가 여러 decision step에서 사용되도록 하겠다는 것을 의미한다. P[0]의 경우 모든 원소의 값을 1로 초기화하며 사용하지 않을 feature가 존재할 경우 P[0]의 해당 원소들을 0으로 초기화하면 된다. 마지막으로 P[i-1]과 $h_ia[i-1]$의 곱에 sparsemax normalization(Martins and Astudillo 2016)을 취한다. Feature selection을 더욱 sparse하게 하기 위해서 loss에 sparsity regularization term(Grandvalet and Bengio 2004)을 추가했다고 한다.
Sparsemax란 무엇인가? (https://arxiv.org/pdf/1602.02068.pdf)
Softmax는 아마 익숙할 것이다. 어떠한 벡터 z의 softmax 연산 결과값은

이다. 결과 벡터의 각 원소는 0보다 크고 원소의 합은 1이기 때문에 확률 벡터를 모델링하는데 많이 사용된다. 그러나 softmax의 문제점은 모든 원소의 값이 0보다 크다는, 한 마디로 sparse하지 않다는 데에 있다. 발생 가능성이 없는 사건의 확률도 0보다 큰 값을 갖게 된다. 본 논문에서처럼 각 decision step에서 필요한 feature만 select하고 싶은 상황에서 softmax를 사용하면 불필요한 feature에도 작지만 0이 아닌 가중치가 붙어 함께 고려되기 때문에 연산량 낭비가 발생한다. 이러한 단점으로 인해 sparsemax가 대신 사용되었다.

벡터 z에 sparsemax 연산을 수행한다는 것은 한마디로 위의 식처럼 z를 probability simplex에 Euclidean projection을 하겠다는 것을 의미한다. Probability simplex란 차원이 z와 같고 원소의 합이 1이며 각 원소가 0 이상인 벡터의 집합을 의미한다. 즉, z와 차원이 같은 확률 벡터의 집합이다. Euclidean projection이란 probability simplex에 속하는 벡터 중에서 z와 L2-distance가 가장 작은 벡터를 찾겠다는 것을 의미한다. 이렇게 찾은 벡터 p는 당연히 확률 벡터의 조건을 만족하고 probability simplex의 경계에 속할 가능성이 높기 때문에 웬만해서는 0인 원소가 많은 sparse vector이다. Sparsemax(z)는 아래의 Algorithm 1을 통해 closed-form으로 구할 수 있다.

경계값 tau(z)를 구한 후 그보다 값이 큰 z의 원소들의 경우 tau를 빼고, 그보다 값이 작은 원소들의 경우 0으로 값을 바꾸는 것이다.
Feature Processing

마스크 M[i]와 $f$의 곱을 feature transformer $f_i$가 처리하면 d[i]와 a[i]가 나온다. 앞에서 살펴봤듯이 a[i]는 다음 decision step에서 mask M[i+1]을 구하는데 사용된다. d[i]는 최종 결정을 내리는데 이바지한다.

파라미터를 절약하기 위하여 feature transformer는 위의 그림에서처럼 첫 두 layer는 모든 decision step에서 동일한 파라미터를 학습하고 그 다음 두 layer에서는 decision step마다 다른 파라미터를 학습한다. 각 layer는 하나의 fully-connected layer와 batch normalization, GLU(gated linearu unit) activation 함수로 이루어졌다. Layer들은 안정성을 위하여 루트 0.5로 normalize한 residual connection으로 연결되었다.
Output Mapping

각 decision step에서 얻은 d[i]에 ReLU를 적용한 후 전부 합하여 벡터 $d_{out}$을 구한다. 이에 linear 연산 $W_{final}$을 적용하면 최종 output이 나온다.
정리하자면 각 decision step마다 다른 feature들을 select하여 d[i]를 계산한다. 그리고 d[i]의 합을 구하여 최종 결정을 내린다는 것은 각 feature combination마다 중요도를 다르게 부여하여 결정에 반영한다는 의미로 해석할 수 있다. Summation 연산 전에 ReLU를 적용함으로써 0보다 작은 d[i]의 원소들은 연산에서 제외되고, 이는 최종 결정을 내리는데 있어서 불필요한 요소들은 제외한다는 의미로 해석할 수 있다.
'추천시스템' 카테고리의 다른 글
| Continual Learning in Recommender Systems (0) | 2022.08.28 |
|---|---|
| 랭킹 최적화 문제 (0) | 2022.07.18 |
| Sequential Recommendation과 GNN (0) | 2022.01.18 |
| 추천시스템과 GNN(Graph Neural Network) (0) | 2022.01.18 |
| DQN 기반 추천시스템 (0) | 2022.01.18 |



