유저가 선택할 아이템을 예측하여 노출시키는 추천시스템이 있는 반면 여러 아이템을 유저의 관심도에 따라 랭킹, 즉 순위를 매겨서 노출시키는 추천시스템이 있다. 전자의 경우 웹 사이트의 특정 영역에 뜨는 광고를 생각하면 되고 후자의 경우 넷플릭스나 유튜브의 동영상 추천을 생각하면 될 것 같다. 전자의 경우 regression이나 classification 문제로 비교적 쉽게 풀리지만 후자의 경우 명확히 regression 혹은 classification 문제로 정의하기 어렵다.
추천 풀에 있는 각 아이템마다 유저의 관심도 점수가 있다고 생각해보자. 당연히 유저가 관심가질만한 아이템을 먼저 보여주는 것이 유리하기 때문에 점수가 큰 아이템부터 순서대로 보여주는 것이 맞을 것이다. $n$개의 아이템이 있을 때, ground-truth 점수를 $y_1, y_2, ..., y_n$, 예측 점수를 $s_1, s_2, ..., s_n$이라고 하자. 만약 이 문제를 regression 문제로 정의한다면 loss function을 아마 다음과 같이 정의하게 될 것이다.

그러나 이 loss function은 결코 랭킹 문제를 풀기 위하여 적합하지 않다. 중요한 것은 $s_1, s_2, ..., s_n$의 상대적 순서를 맞추는 것이지 $y_1, y_2, ..., y_n$과의 절대적 값의 차이를 최대한 줄이는 것이 아니다. 위의 loss function을 최소화한 예측 점수 벡터가 순서를 가장 잘 맞춘 것이라는 보장이 전혀 없다.
따라서 랭킹 문제를 regression과는 다른 방식으로 풀어야 한다. 그렇다면 과연 랭킹 문제는 어떠한 objective/metric에 대하여 최적화해야되는 것일까? 이는 결국 머신러닝/딥러닝 기반 추천시스템을 구축할 때 필수적인 loss function을 어떻게 정의하냐로 직결되기 때문에 꼭 심도 있게 다루어야할 문제다. 이번 포스트에서는 추천시스템 랭킹 문제에 활용할 수 있는 다양한 최적화 방법 및 loss function들을 다룰 것이다.
1. Top-K Correction
이 방식은 강화학습을 이용한 Top-K 추천시스템에서 소개한 논문에서 제안된 방식이다. 랭킹이랑은 다른 문제지만 하나가 아닌 다수의 아이템을 추천한다는 데서 비슷해서 한번 가져와봤다. 강화학습 자체는 본 포스트와 관련이 없기 때문에 reward-to-go $R$을 아이템의 클릭 여부에 따라 1/0의 값을 갖는 immediate reward로 대체하고 off-policy correction 부분은 일단 무시하자.
기본적으로 딥러닝 모델은 마지막에 softmax activation을 통해 각 아이템의 클릭 확률을 예측한다. 1개의 가장 좋은 아이템만을 추천하는 문제에서 loss는 $-\sum_{i=1}^{i=n}y_ilog(\pi_{\theta}(i))$가 되고 gradient는 $\sum_{i=1}^{i=n}y_i\nabla log(\pi_{\theta}(i))$가 될것이다. Ground-truth 랭킹 점수 $y_i$는 단순 클릭 label로, 하나의 클릭된 아이템에 대해서는 1, 나머지에 대해서는 0의 값을 가질 것이다. 강화학습 formulation에서는 $y_i$가 immediate reward의 역할을 한다고 볼 수 있다.
그러나 문제는 가장 좋은 1개의 아이템을 추천하는 것이 아니라 $K$개의 아이템을 추천하는 것이다. 이를 위해 loss와 gradient를 변형해보자.
가장 좋은 $K$개의 아이템을 선택한다고 하면 $i$번째 아이템의 클릭 확률이 어떻게 될까? 확률 $\pi_{\theta}(1), ..., \pi_{\theta}(n)$에 따라 각 아이템을 독립적으로 샘플링하고 중복된 아이템은 제거하는 방식으로 $K$개의 아이템을 선택한다고 하자. 그러면 어떠한 아이템 $i$가 선택된 $K$개의 아이템 중 하나일 확률은 다음과 같다.
$\alpha_{\theta}(i) = 1 - (1-\pi_{\theta}(i))^K$
대입하면 loss는 아래와 같이 변형된다.
$-\sum_{i=1}^{i=n}y_ilog(\alpha_{\theta}(i))$
이에 따라 gradient는 아래와 같이 변형된다.
$\sum_{i=1}^{i=n}K(1-\pi_{\theta}(i))^{K-1}y_i\nabla log(\alpha_{\theta}(i))$
기존 gradient에 비해 각 $i$에 대하여 $K(1-\pi_{\theta}(i))^{K-1}$이 곱해진 것을 확인할 수 있다. 이는 한 아이템에 추천 확률이 모일 경우, 즉 예측 확률 $\pi_{\theta}$가 1에 가까워질 경우 gradient가 0에 가까워져 더 이상 추천 확률이 증가하지 않도록 한다. 이에 따라 추천 확률이 특정 아이템에 집중되지 않고 여러 아이템에 분산된다.

위의 그래프는 논문의 시뮬레이션 실험 결과를 가져온 것으로 아이템 1~10 중에서 1을 추천했을 때 리워드가 10, 2를 추천했을 때 리워드가 9, 그리고 나머지가 1일 때, 일반적인 loss를 적용하였을 때와 Top-2 correction을 적용했을 때의 $\pi_{\theta}(i)$를 나타낸 것이다. 좌측 그래프에서는 가장 좋은 아이템에만 추천 확률이 몰려 두개의 아이템을 추천할 때 두번째로 좋은 아이템인 아이템 2가 함께 추천될 확률이 희박해진다. 반면 Top-2 correction을 적용하였을 경우 아이템 1과 2 다 높은 추천 확률을 보이고, 아이템 1과 아이템 2의 랭킹이 제대로 이루어졌다.
따라서 여러 개의 아이템을 한번에 추천하고 가장 좋은 아이템부터 순서대로 노출시키고 싶을 때 위와 같은 loss function correction이 유용할 것이라고 기대된다. 더불어 ground truth 랭킹 점수가 단순히 클릭 여부임에도 적용할 수 있기 때문에 여러 문제에 확장 가능하다.
2. Ranking Metric에 기반한 Loss Function
이제부터는 The LambdaLoss Framework for Ranking Metric Optimization 라는 논문에 소개된, 랭킹 metric에 기반한 여러 loss function들을 살펴보자.
2.1 Simple Loss Function

위에 loss function은 $s_i$의 값을 정확히 맞추기 보단 $s_i$들의 순서를 맞추는데 초점을 두었다는 것을 직관적으로 알 수 있다. $y_i > y_j$인데 $s_i < s_j$인, 랭킹이 어긋난 $(i,j)$ 쌍들에 대하여 패널티를 주는 것이다. 본 loss function은 cross-entropy에 기반을 두었으며 $\sigma$는 hyperparameter이다.
2.2 NDCG 최적화
NDCG는 랭킹 성능을 측정할 수 있는 대표적인 metric이다. 더불어 높은 순위에 있는 아이템들의 성능을 더 강조하기 때문에 랭킹 문제에서 최적화하기 적합하다. 값이 클수록 랭킹이 잘 된 것이다. NDCG를 계산하기 위해서는 먼저 아이템들이 추천 점수 $s$의 내림차순으로 순위 $i = 1, 2, ..., n$가 매겨졌다고 가정한다. 그럼 NDCG는 아래와 같이 계산된다.

maxDCG는 상수값으로 $y=s$, 즉 ground truth 점수 $y_1, ..., y_n$에 따라 아이템 순서를 매겼을 때의 $\sum_{i=1}^n\frac{2^{y_i} - 1}{log_2(1+i)}$ 값이다.
-NDCG를 loss function으로 사용할 수 있으면 참 좋겠지만... 이 값에 gradient descent를 적용할 수가 없다는 문제가 있다. NDCG를 구하기 위해서는 점수들을 소팅하여 순위를 매겨야하기 때문이다. 따라서 머신러닝/딥러닝 추천시스템에서 NDCG를 직접적으로 최적화하는 것은 불가능하다.
2.3 LambdaRank
LambdaRank는 NDCG 자체를 최적화 objective로 삼기 보다는 NDCG 기반으로 loss를 조정하고자 한다.

where

$\triangle NDCG(i,j)$는 아이템 $i$와 $j$의 순서가 서로 바뀌었을 때 NDCG 값의 차이다. 아이템 $i$와 $j$의 순서가 뒤바꼈을 때 그만큼 더 곱해서 패널티를 주는 것이다.
실험적으로 LambdaRank는 랭킹 문제에 있어서 좋은 성능을 보여왔다. 그러나 본 논문 이전까지는 LambdaRank의 수학적 해석에 대한 논란이 많았다.
2.3.1 LambdaRank의 수학적 해석
Maximum likelihood 기법에 의해 우리는 예측 점수 $s = [s_1, ..., s_n]$와 $y = [y_1, ..., y_n]$에 대하여 $p(y|s)$를 극대화하고 싶을 것이고, 따라서 아래의 negative log likelihood를 사용하는 것이 합당하다.
$l(y, s) = -log_2p(y|s)$
Binary classification 문제에서 많이 하듯이, 아이템 $i$의 실제 점수 $y_i$가 $j$의 실제 점수 $y_j$보다 클 확률을 아래와 같이 모델링한다고 하자.

그렇다면 negative log likelihood는 아래와 같아진다.

이로써 2.1의 loss function이 어떻게 나왔는지 알 수 있다.
여기서 문제를 더 확장해보자. 예측 점수 벡터 $s$에 따라 아이템의 순서 $\pi$가 하나로 결정되는 것이 아니라 그의 분포 {$p(\pi | s) | \pi \in \Pi$}가 결정되고, 실제 점수 벡터 $y$는 $\pi$에 dependent하다고 하자. 그렇다면 negative log likelihood를 아래와 같이 전개할 수 있다.
$l(y, s) = -log_2p(y|s) = -log_2p(y|s,\pi)p(\pi|s)$
$\pi_i$와 $\pi_j$를 순서 $\pi$에서 아이템 $i$, $j$ 각각의 순위라고 하자. 그렇다면 아이템 $i$의 실제 점수가 $j$보다 클 확률을 아래와 같이 모델링해볼 수 있다.

여기서 $G_i = \frac{2^{y_i} - 1}{maxDCG}$, $D(\pi_i) = log_2(1+\pi_i)$가 된다. 위와 같이 모델링하여 negative log likelihood는 아래와 같이 구할 수 있다.

2.3.1.1 EM Algorithm에 의한 최적화
지금까지 구한 loss function을 EM(Expectation Maximization) 기법으로 최적화할 수 있다. EM 알고리즘에서는 iteration $1, ..., t, ..., T$에 대하여 E-step과 M-step을 반복한다. 이 알고리즘은 local minimum에 대한 수렴을 보장해준다. 본 문제에서 E-Step과 M-step을 아래와 같이 정의한다.
- E-Step : 모델로부터 아이템 순서에 대한 분포 $P^{(t)}(\pi|s)$를 추정한다.
- M-Step : 학습 데이터에 대한 negative loss likelihood $l(y,s)$를 최적화하여 모델을 업데이트한다.
여기서 모든 가능한 순서 $\pi$에 대하여 $P(\pi|s)$를 구하고 각각에 대해 다 계산한다고 생각하면 굉장히 머리가 아파진다. 다행히 일부 순서만 샘플링해서 모델 업데이트를 하도록 하는 몬테카를로 기법이 있다. $P(\pi|s)$를 다음의 hard assignment distribution $H(\pi|s)$로 정의하면 계산량을 더욱 줄일 수 있다.

여기서 $\hat{\pi}$는 $s$에 대한 내림차순으로 정의한다. Negative log likelihood는 아래와 같은 식으로 완성된다.

이제 LambdaRank는 위의 loss를 최적화하는 EM 기법이라는 것을 보일 수 있다. E-step에서는 모델을 통해 예측 점수 벡터 $s$를 계산하고 이를 바탕으로 $\hat{\pi}$를 얻는다. M-step에서는 학습 데이터에 대한 loss를 구하여 모델을 업데이트한다. Loss는 다음과 같이 정리된다.

2.3에서 본 LambdaRank의 loss function이 나오는 것을 확인할 수 있다.
2.4 랭킹 Metric을 최적화하는 Loss Function
보기와는 달리 LambdaRank는 NDCG와 관련은 있지만 NDCG를 자체를 최적화하지 않는다. 그래서 저자들은 주요 랭킹 metric을 최적화하는 loss function을 도출한다. 도출 과정에서 아래 부등식이 이용된다.

아래 그림을 보면 이 부등식이 더 쉽게 납득될 것이다.

2.4.1 Average Relevance Position (ARP)
아이템들의 순서가 $\hat{\pi}$일 때 $i$번째 아이템의 실제 점수를 $y_i$, 예측 점수를 $s_i$라고 하자.
먼저 ARP는 값이 작을수록 랭킹 성능이 좋은 메트릭으로, 아래 수식과 같이 구한다.

$\hat{\pi}$의 정의에 따라 $i$를 다음과 같이 나타낼 수 있다.

이를 대입하여 ARP를 다음과 같이 전개할 수 있다.

여기서 $C_1$은 $\sum_{i=1}^ny_i$로 상수이다. 따라서 $\sum_{i=1}^n\sum_{j=1}^ny_ilog_2(1+e^{-\sigma(s_i-s_j)})$를 ARP의 upper bound로 볼 수 있고, 이를 최적화함으로써 간접적으로 ARP를 최적화할 수 있다.
이에 따라 loss function을 다음과 같이 정의할 수 있다.

저자들은 ARP의 또 다른 upper bound를 구하여 두 번째 loss function를 제시한다. 전개 방식은 아래와 같다.

같은 원리로 도출되는 loss function은 $l(y,s) = -\sum_{y_i>y_j}log_2\sigma_{\pi}(\frac{1}{1+e^{-\sigma(s_i-s_j)}})^{|y_i-y_j|}H(\pi|s)$가 된다.
2.4.2 NDCG
NDCG는 ARP와 달리 최대화해야하는 metric이기 때문에 NDCGcost를 다음과 같이 정의한다.

$D_i - 1=log_2(1+i)-1\leq i-1$이므로 NDCGcost의 upper bound를 아래와 같이 구할 수 있다.

마찬가지로 NDCGcost를 직접적으로 최소화하기보다는 그 upper bound를 최소화하는 것을 목표로 한다면 아래 loss function을 최적화하는 EM 알고리즘을 세울 수 있다.

저자들은 여기서 더 나아가 NDCGcost에 대하여 더 tight한 upper bound를 구하고자 했다. 우선 chain rule에 대하여 다음이 성립한다.

$\delta_{ij} = \delta_{ji}$가 성립한다는 것은 쉽게 알 수 있다. $\delta_{ii} = 0$이라고 정의하자. 그러면 아래와 같이 NDCGcost의 upper bound가 도출된다.

where


이 둘 다 한 번의 M-step 내에서는 상수이다. 그렇다면 loss function을 아래와 같이 세울 수 있다.
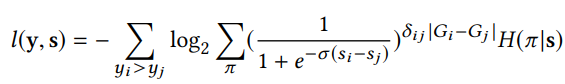
$G_i$, $D_i$에 다른 수식을 대입하여 다양한 랭킹 metric에 이 loss function을 적용할 수 있다.
'추천시스템' 카테고리의 다른 글
| 추천시스템의 분류 (0) | 2022.10.21 |
|---|---|
| Continual Learning in Recommender Systems (0) | 2022.08.28 |
| 정형 데이터를 다루기 위한 Neural Network (0) | 2022.01.18 |
| Sequential Recommendation과 GNN (0) | 2022.01.18 |
| 추천시스템과 GNN(Graph Neural Network) (0) | 2022.01.18 |


