이번 포스트에서는 위험 포트폴리오의 구성을 결정하는 방법에 대하여 알아보자. 간단하게 채권 펀드와 주식 펀드, 이 두 개의 위험 자산만으로 위험 포트폴리오를 구축한다고 가정하자.
용어 정리
금융 상품의 스펙을 구하기 위해서는 우선 미래 시나리오(ex. 불황, 호황, 정상 성장, etc.)를 여러 개 가정하고 각 시나리오에서 예상되는 금융 상품의 수익률을 구한다. 총 \(n\)개의 시나리오가 있다고 가정하고 각 시나리오의 인덱스를 \(i\)로 표기하자.
\(r_B(i)\) : 채권 펀드의 시나리오 \(i\)에서의 수익률
\(r_S(i)\) : 주식 펀드의 시나리오 \(i\)에서의 수익률
\(E(r_B)\) : 채권 펀드의 기대 수익률
\(E(r_S)\) : 주식 펀드의 기대 수익률
\(\sigma_B\) : 채권 펀드 수익률의 표준편차
\(\sigma_S\) : 주식 펀드 수익률의 표준편차
\(p(i)\) : 시나리오 \(i\)가 발생할 확률
\(Cov(r_S, r_B)\) : 채권 펀드와 주식 펀드의 공분산 (\(\sum_{i=1}^{n}p(i)[r_S(i)-E(r_S)][r_B(i)-E(r_B)]\))
\(\rho_{SB}\) : 채권 펀드와 주식 펀드의 상관계수 (\(\frac{Cov(r_S, r_B)}{\sigma_B\sigma_S}\))
\(\rho_{SB}\)은 -1과 1 사이의 값이다. 그 값이 양수라면 채권 펀드와 주식 펀드의 수익률이 같은 방향으로 움직인다(함께 증가, 함께 감소)는 뜻이고 음수라면 반대 방향으로 움직인다는 뜻이다. 절댓값이 클수록 둘 사이의 상관관계가 뚜렷하다고 해석된다. \(\rho_{SB}\)가 0이면 두 자산의 수익률이 서로 관계가 없다는 뜻이다.
\(r_P\) : 위험 포트폴리오의 수익률
\(E(r_P)\) : 위험 포트폴리오의 기대 수익률
\(\sigma_P\) : 위험 포트폴리오 수익률의 표준편차
\(w_B\) : 위험 포트폴리오에서 채권 펀드가 차지하는 비율 (= \(1-w_S\))
\(w_S\) : 위험 포트폴리오에서 주식 펀드가 차지하는 비율 (= \(1-w_B\))
\(r_f\) : 무위험수익률
최적의 포트폴리오
평균-분산 최적화(Mean-Variance Optimization: MVO)
결국 투자자는 리스크를 줄이면서 높은 수익률을 얻을 수 있는 최적의 \(w_B\) 값을 찾고 싶을 것이다. 위험 포트폴리오의 기대 수익률과 수익률의 분산을 구하는 식은 다음과 같다.
$E(r_P) = w_BE(r_B) + w_SE(r_S)$
$\sigma_P^2 = (w_B\sigma_B)^2 + (w_S\sigma_S)^2 + 2(w_B\sigma_B)(w_S\sigma_S)\rho_{BS}$
Case 1 : \(\rho_{SB} = 1\)
이 경우 위험 포트폴리오의 표준편차는 채권 펀드와 주식 펀드의 표준편차의 가중평균이 된다.
$\sigma_P = w_B\sigma_B + w_S\sigma_S$
따라서 분산투자로 인한 이득이 전혀 없다.
Case 2 : \(\rho_{SB} < 1\)
이 경우 위험 포트폴리오의 표준편차는 채권 펀드와 주식 펀드의 표준편차의 가중평균보다 작다.
$\sigma_P < w_B\sigma_B + w_S\sigma_S$
따라서 분산투자로 인해 이득을 볼 수 있다. \(\rho_{SB}\)가 작을수록 분산투자로 보는 이득이 더 커진다. 직관적으로 상관계수가 음수일 때를 생각해자. 두 자산의 수익률이 반대로 움직이므로 불경기에 한 자산의 수익률이 감소하는 대신 다른 자산의 수익률은 증가하게 되어 손실과 리스크를 줄일 수 있을 것이다.
특히 \(\rho_{SB}\)가 -1인 경우 포트폴리오의 표준편차는 아래와 같다.
$\sigma_P = \left|w_B\sigma_B - w_S\sigma_S\right|$
따라서 $w_B\sigma_B = w_S\sigma_S$가 되도록 하면 포트폴리오의 표준편차가 0이 되도록, 즉 리스크가 전혀 없도록 할 수 있다. 물론 현실에서 잘 일어나지 않는 상황이다.
\(\rho_{SB} < 1\)인 경우 투자기회집합은 일반적으로 아래와 같은 포물선 형태이다.

투자자는 높은 기대수익률(\(E(r_P)\))과 낮은 표준편차(\(\sigma_P\))를 원하므로 평면에서 좌상단(northwest)에 있는 포트폴리오를 원할 것이다. 보다시피 투자기회집합에서 최소분산 포트폴리오 아래에 있는 포트폴리오는 최소 분산 포트폴리오보다 수익률은 낮으면서 위험은 더 크기 때문에 고려할 필요가 없다. 최소분산 포트폴리오 위에 있는 포트폴리오들은 아직 우열을 가리기 힘들다.
1편에서 배운 무위험자산을 포트폴리오에 추가해보자. 1편 내용을 되새겨보자면 무위험자산과 위험 포트폴리오를 합친 완성 포트폴리오의 투자기회집합은 자본배분선(CAL)이라는 직선이 된다. 위험 포트폴리오 $P$를 선택했을 때 이 직선은 $(0, r_f)$와 $(\sigma_P, E(r_P))$를 지나게 된다. 그러므로 투자자는 포물선 위의 점과 $(0, r_f)$를 잇는 수많은 직선 중에서 하나를 선택해야한다. 또한, 자본배분선의 기울기는 샤프 비율이며 샤프 비율이 높을수록 위험 대비 기대수익률이 높은 것이기 때문에 효율적인 포트폴리오다. 따라서 투자자는 포물선 위의 점과 $(0, r_f)$를 잇는 직선 중에서 기울기가 가장 큰 것을 찾아야 한다는 결론이 나온다. 이를 어떻게 찾을까?
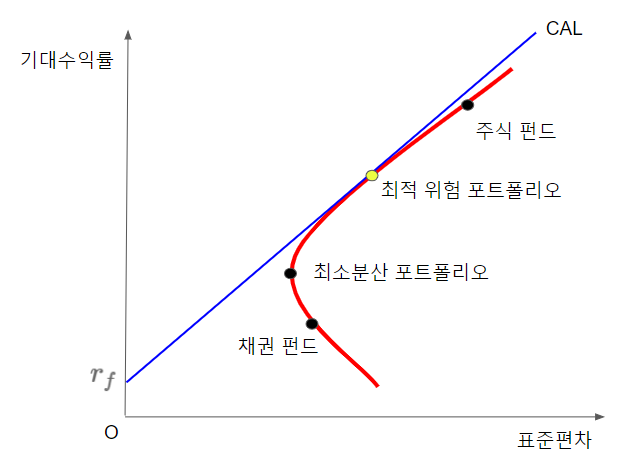
바로 자본배분선이 포물선에 접할 때 그 기울기가 가장 크다. 그 접점에 해당하는 위험 포트폴리오를 최적 위험 포트폴리오라고 부른다. 최적 위험 포트폴리오에 해당하는 $w_B$와 $w_S$ 값은 스스로 계산해보자.
분리 속성
최적 위험 포트폴리오를 찾은 다음 투자자는 본인의 위험 회피도에 따라 무위험자산과 위험 포트폴리오 간의 예산 배분 비율을 결정하게 된다. 최적 위험 포트폴리오는 투자자의 성향과 무관하게 계산으로 구해지는 반면 무위험자산과 위험 자산 간의 비율은 답이 없고 오로지 투자자의 선택에 달렸다.
정리하자면 완성 포트폴리오를 구축하는 과정은 평균-분산 최적화를 통해 최적 위험 포트폴리오를 찾는 단계와 무위험자산과 위험 포트폴리오 간의 비율을 결정하는 단계로 나뉜다. 이렇게 포트폴리오 구축이 서로 독립적인 두 단계로 나뉘는 특성을 분리 속성이라고 부른다.
'금융 AI' 카테고리의 다른 글
| 포트폴리오 이론 3편 - 여러 위험 자산으로의 확장 (0) | 2022.02.06 |
|---|---|
| 포트폴리오 이론 1편 - 위험 자산과 무위험 자산 (0) | 2022.02.05 |
| 액티브와 패시브 투자 전략 (0) | 2022.02.04 |
| 로보어드바이저(Robo-Advisor)란? (0) | 2022.01.31 |
| 알파와 베타 (0) | 2022.01.30 |


